6.2 Voorbeeld
R bevat een dataset van een experiment over effect van vitamine C op tandgroei. De vitamine werd toegediend aan huiscavia’s (Cavia porcellus)in drie doses (dose) (0,5, 1 en 2 mg/dag) op twee verschillende manieren (supp): sinaasappelsap of vitamine C druppels. De lengte van odontoplasten (groeicellen van de tanden) werden gemeten.
De data importeren:
data("ToothGrowth") Checken wat de structuur is:
str(ToothGrowth)## 'data.frame': 60 obs. of 3 variables:
## $ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
## $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
## $ dose: num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...De verklarende variabelen supp en dose willen we in de statistische toets behandelen als een factor (categoriedata). Maar zoals je in bovenstaande overzicht ziet staan, wordt dose niet als factor herkend. Dat kunnen we oplossen met:
ToothGrowth$dose <- factor(ToothGrowth$dose)Ook handig om te checken hoeveel herhalingen er zijn gedaan per behandeling:
table(ToothGrowth$supp, ToothGrowth$dose)##
## 0.5 1 2
## OJ 10 10 10
## VC 10 10 10Zo te zien dus een mooi gebalanseerd full factorial design.
Altijd goed om eerst de data te bekijken met een paar figuren. Als eerste een boxplot:
library(tidyverse)
ToothGrowth %>%
ggplot(aes(dose, len, colour = supp)) +
geom_boxplot() +
theme_classic()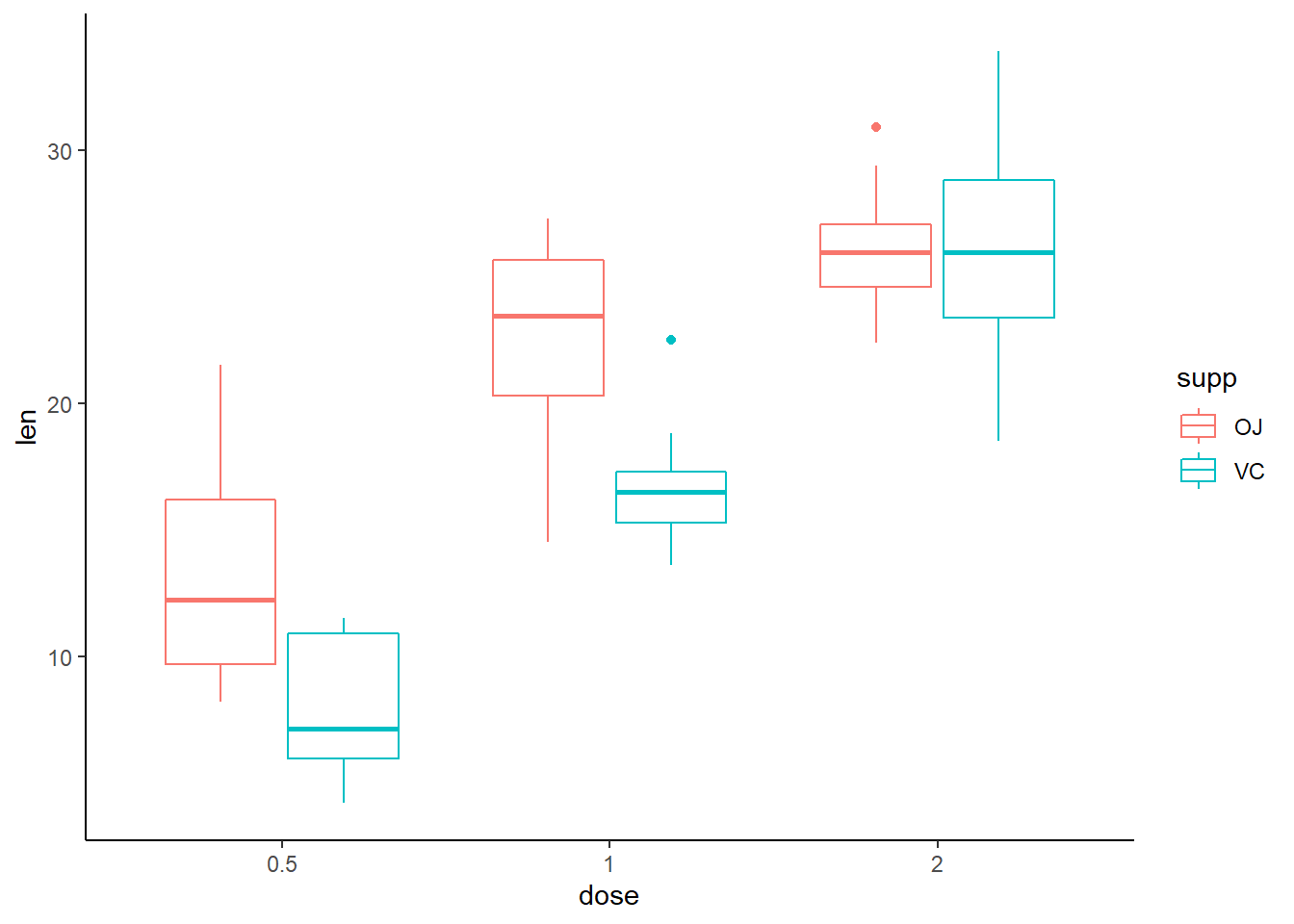
Bij de lagere doses geeft vitamine C (VC) kortere odontoplasten (len) dan sinaasappelsap (OJ), maar niet bij de hoogste dosis. Er is dus mogelijk een interactie-effect. Verder zie je dat hogere dosis consequent leidt tot langere odontoplasten. Dat duidt op een hoofdeffect van dose.
Een lijnfiguur kan het nog duidelijker maken (nu met dose en supp omgedraaid):
ToothGrowth %>%
ggplot(aes(supp, len, colour = dose)) +
geom_point(stat = 'summary', fun.y=mean, size =3) +
geom_jitter(width=0.1) +
stat_summary(aes(group = dose), fun.y=mean, geom='line') +
theme_classic()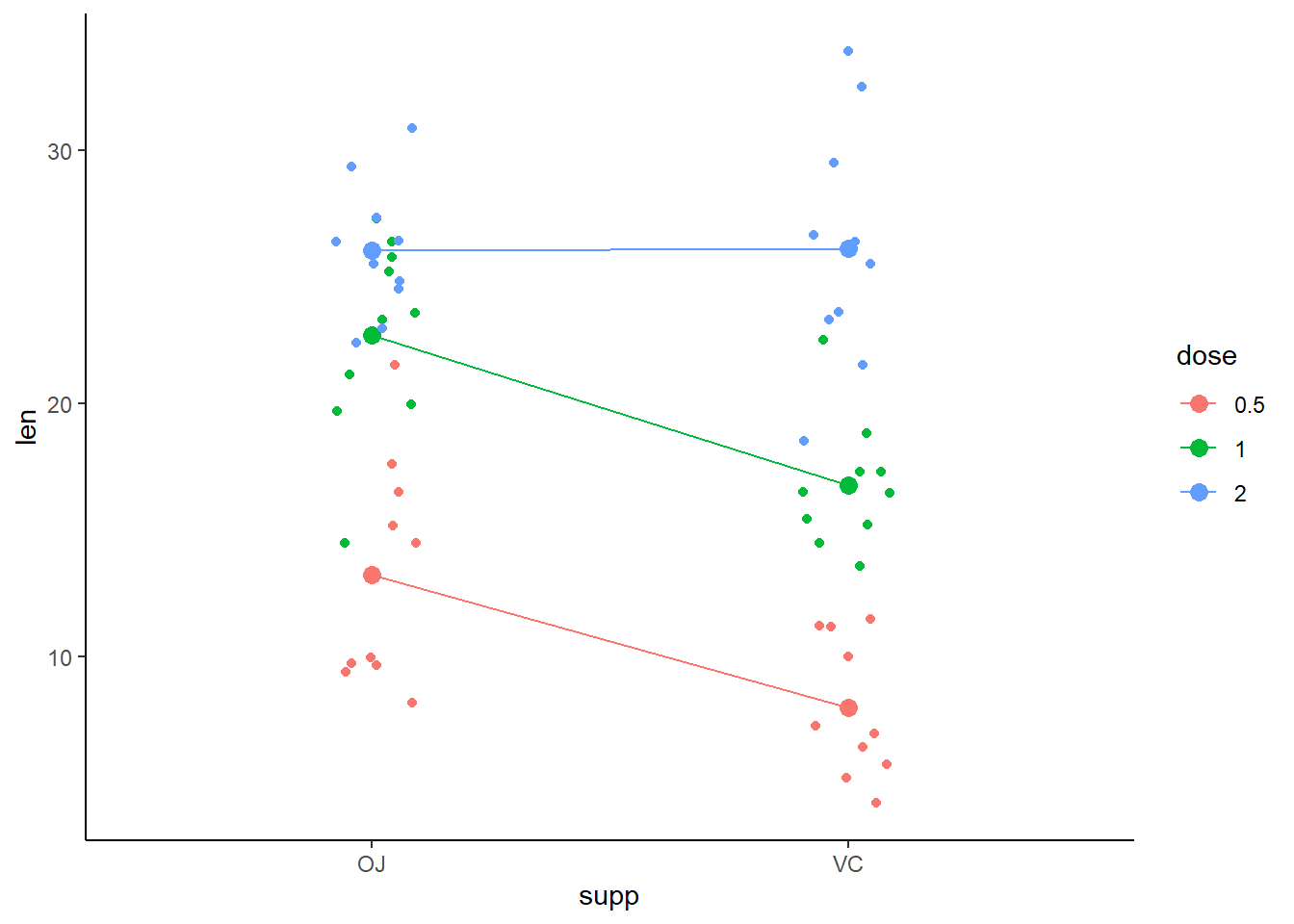
Het effect van OJ naar VC is bij dosis 0,5 en 1 hetzelfde, maar afwezig bij dosis 2. Een duidelijke aanwijzing voor een interactie-effect.
Met een two-way ANOVA (meervoudige variantie-analyse) kunnen we testen of dat inderdaad zo is:
fit <- lm(len ~ dose * supp, data=ToothGrowth)
anova(fit)## Analysis of Variance Table
##
## Response: len
## Df Sum Sq Mean Sq F value Pr(>F)
## dose 2 2426.43 1213.22 92.000 < 2.2e-16 ***
## supp 1 205.35 205.35 15.572 0.0002312 ***
## dose:supp 2 108.32 54.16 4.107 0.0218603 *
## Residuals 54 712.11 13.19
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Dose en supp hebben allebei een significant hoofdeffect (p < 0,05), maar beide hebben ook een interactie-effect (dose:supp).
We kunnen dus de volgende nulhypotheses verwerpen:
\(H_{0}: \mu_{OJ} = \mu_{VC}\)
ten faveure van:
\(H_{1}: \mu_{OJ} \neq \mu_{VC}\)
En:
\(H_{0}: \mu_{D0.5} = \mu_{D1} =\mu_{D2}\)
ten faveure van:
\(H_{1}:\) tenminste twee van de drie \(\mu\)’s zijn verschillend.
Dat waren de hoofdeffecten. Voor de interactie-effecten hebben we de volgende nulhypothese:
H0: er is geen sprake van een interactie-effect waarbij het effect van supp op len afhangt van welke dosis wordt gehanteerd of andersom, waarbij het effect van dosis op de groei afhangt van welke supp wordt gehanteerd.
ten faveure van:
H1: er is sprake van een interactie-effect
Met emmeans kunnen we én de gemiddelden per combi uitrekenen en posthoctoetsen uitvoeren.
als eerste een van de hoofdeffecten:
library(emmeans)
emmeans(fit, specs = pairwise ~dose)## $emmeans
## dose emmean SE df lower.CL upper.CL
## 0.5 10.6 0.812 54 8.98 12.2
## 1 19.7 0.812 54 18.11 21.4
## 2 26.1 0.812 54 24.47 27.7
##
## Results are averaged over the levels of: supp
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## dose0.5 - dose1 -9.13 1.15 54 -7.951 <.0001
## dose0.5 - dose2 -15.49 1.15 54 -13.493 <.0001
## dose1 - dose2 -6.37 1.15 54 -5.543 <.0001
##
## Results are averaged over the levels of: supp
## P value adjustment: tukey method for comparing a family of 3 estimatesVervolgens effect van supplement:
emmeans(fit, specs = pairwise ~supp)## $emmeans
## supp emmean SE df lower.CL upper.CL
## OJ 20.7 0.663 54 19.3 22.0
## VC 17.0 0.663 54 15.6 18.3
##
## Results are averaged over the levels of: dose
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## OJ - VC 3.7 0.938 54 3.946 0.0002
##
## Results are averaged over the levels of: doseEn als laatste de combi’s:
emmeans(fit, specs = pairwise ~dose:supp)## $emmeans
## dose supp emmean SE df lower.CL upper.CL
## 0.5 OJ 13.23 1.15 54 10.93 15.5
## 1 OJ 22.70 1.15 54 20.40 25.0
## 2 OJ 26.06 1.15 54 23.76 28.4
## 0.5 VC 7.98 1.15 54 5.68 10.3
## 1 VC 16.77 1.15 54 14.47 19.1
## 2 VC 26.14 1.15 54 23.84 28.4
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## dose0.5 OJ - dose1 OJ -9.47 1.62 54 -5.831 <.0001
## dose0.5 OJ - dose2 OJ -12.83 1.62 54 -7.900 <.0001
## dose0.5 OJ - dose0.5 VC 5.25 1.62 54 3.233 0.0243
## dose0.5 OJ - dose1 VC -3.54 1.62 54 -2.180 0.2640
## dose0.5 OJ - dose2 VC -12.91 1.62 54 -7.949 <.0001
## dose1 OJ - dose2 OJ -3.36 1.62 54 -2.069 0.3187
## dose1 OJ - dose0.5 VC 14.72 1.62 54 9.064 <.0001
## dose1 OJ - dose1 VC 5.93 1.62 54 3.651 0.0074
## dose1 OJ - dose2 VC -3.44 1.62 54 -2.118 0.2936
## dose2 OJ - dose0.5 VC 18.08 1.62 54 11.133 <.0001
## dose2 OJ - dose1 VC 9.29 1.62 54 5.720 <.0001
## dose2 OJ - dose2 VC -0.08 1.62 54 -0.049 1.0000
## dose0.5 VC - dose1 VC -8.79 1.62 54 -5.413 <.0001
## dose0.5 VC - dose2 VC -18.16 1.62 54 -11.182 <.0001
## dose1 VC - dose2 VC -9.37 1.62 54 -5.770 <.0001
##
## P value adjustment: tukey method for comparing a family of 6 estimates