7.1 Binomiale data (logistische regressie)
Als eerste een voorbeeld van een situatie met als verklarende variabele een nominale variabele.
## Warning: package 'readxl' was built under R version 4.1.3## -- Attaching packages --------------------------------------- tidyverse 1.3.1 --## v ggplot2 3.3.6 v purrr 0.3.4
## v tibble 3.1.7 v dplyr 1.0.9
## v tidyr 1.2.0 v stringr 1.4.0
## v readr 2.1.2 v forcats 0.5.1## Warning: package 'ggplot2' was built under R version 4.1.3## Warning: package 'tibble' was built under R version 4.1.3## Warning: package 'tidyr' was built under R version 4.1.3## Warning: package 'readr' was built under R version 4.1.3## Warning: package 'dplyr' was built under R version 4.1.3## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()Hier een voorbeeld van een dataset die je op twee manieren kan benaderen. Als eerste een binomiale variant van een Oneway ANOVA, waarbij dus de verklarende variabele als categorie benaderd wordt.
In ggplot kan je zulke data met een mosaicplot mooi weergeven. Hier een voorbeeldscript:
library(ggmosaic)
tomaat %>%
ggplot() +
geom_mosaic(aes(x=product(tijd), fill = rijp)) +
scale_fill_manual(values = c("green", "red")) +
xlab("tijd (dagen voor oogstijd)") +
ylab("fractie rijp") +
theme(legend.position = "non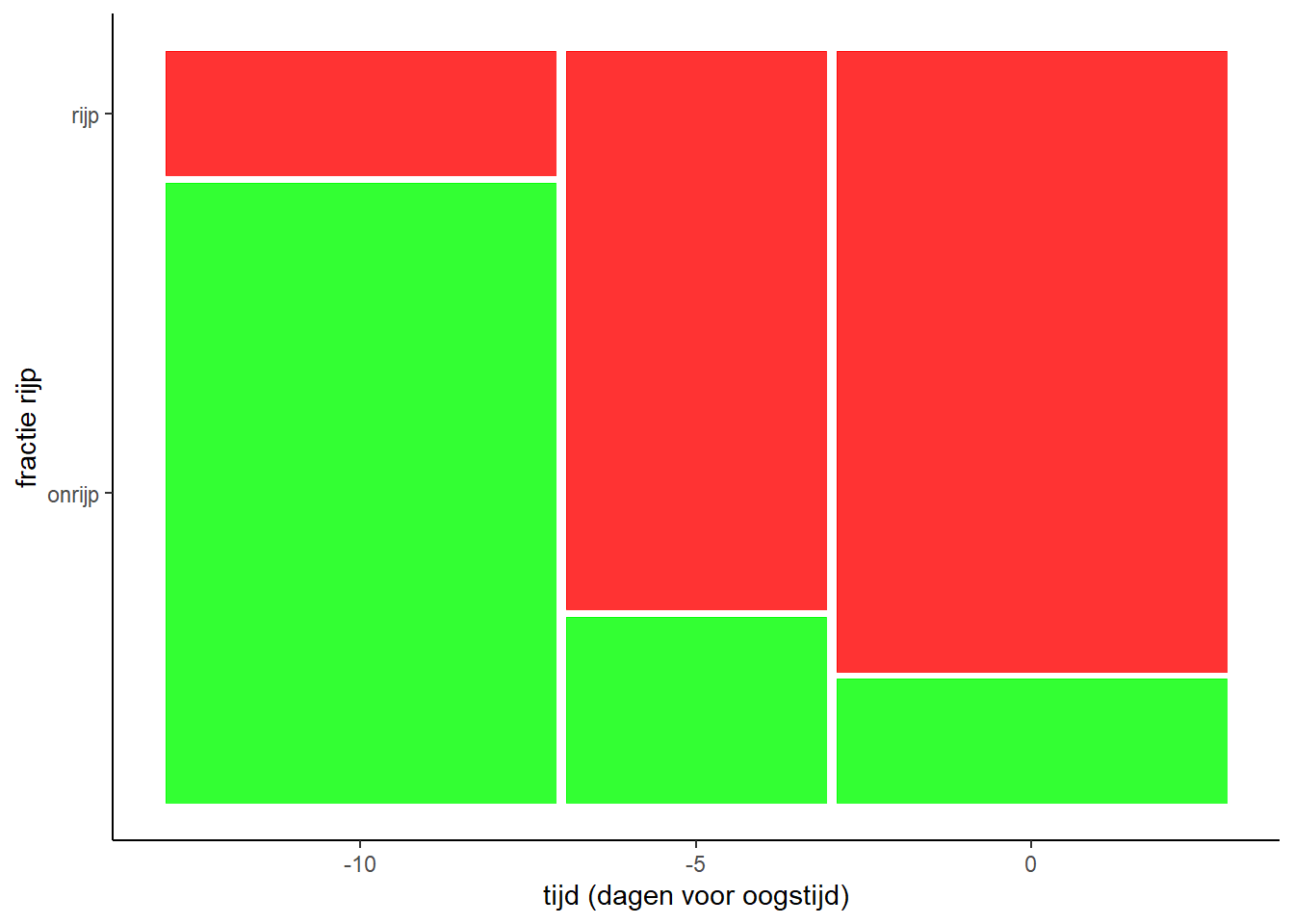e")
Met een Generalized Linear Model kunnen we testen of de oogsttijdstippen van elkaar verschillen.
Voorwaarde is wel dat de responsvariabele bestaat uit enen en nullen.
Daar kunnen we de functie recode() voor gebruiken:
tomaat_num <- tomaat %>%
mutate(rijp = recode(rijp, "onrijp" = 0, "rijp" = 1))Vervolgens zetten we de statistisch model op.
Met het argument family geef je aan om wat voor soort data het bij de responsdata gaat:
fit <- glm(rijp~factor(tijd), family = binomial(), data = tomaat_num)NB: we gebruiken factor(tijd) om te zorgen dat R tijd als categoriedata gebruikt.
Wil je een ‘echte’ Anovatabel (met wat haken en ogen), dan kan je me de functie Anova() uit de package car die tevoorschijn toveren:
car::Anova(fit)## Analysis of Deviance Table (Type II tests)
##
## Response: rijp
## LR Chisq Df Pr(>Chisq)
## factor(tijd) 6.6179 2 0.03655 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Je kan ook de functie summary() gebruiken, die de geschatte waarden voor ieder niveau geeft (in log-odds uitgedrukt):
summary(fit)##
## Call:
## glm(formula = rijp ~ factor(tijd), family = binomial(), data = tomaat_num)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.8930 -0.6039 0.6039 0.6425 1.8930
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.609 1.095 -1.469 0.1418
## factor(tijd)-5 2.708 1.592 1.701 0.0889 .
## factor(tijd)0 3.219 1.549 2.078 0.0377 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 21.930 on 15 degrees of freedom
## Residual deviance: 15.312 on 13 degrees of freedom
## AIC: 21.312
##
## Number of Fisher Scoring iterations: 4Net als bij een gewone ANOVA kan je hier ook een posthoc-toets uitvoeren.
Dat doen we met de functie emmeans() uit de package emmeans:
library(emmeans)
emmeans(fit, specs = pairwise ~ tijd)## $emmeans
## tijd emmean SE df asymp.LCL asymp.UCL
## -10 -1.61 1.10 Inf -3.756 0.538
## -5 1.10 1.15 Inf -1.165 3.362
## 0 1.61 1.10 Inf -0.538 3.756
##
## Results are given on the logit (not the response) scale.
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df z.ratio p.value
## (tijd-10) - (tijd-5) -2.708 1.59 Inf -1.701 0.2046
## (tijd-10) - tijd0 -3.219 1.55 Inf -2.078 0.0945
## (tijd-5) - tijd0 -0.511 1.59 Inf -0.321 0.9448
##
## Results are given on the log odds ratio (not the response) scale.
## P value adjustment: tukey method for comparing a family of 3 estimatesJe kan ook in een glm ook kiezen om als verklarende variabele een numerieke variabele te nemen, zodat je een soort van regressie krijgt.
fit2 <- glm(rijp ~ tijd, family = binomial(), data = tomaat_num)
summary(fit2)##
## Call:
## glm(formula = rijp ~ tijd, family = binomial(), data = tomaat_num)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0802 -0.7021 0.4941 0.6254 1.7443
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.0416 1.1143 1.832 0.0669 .
## tijd 0.3316 0.1597 2.077 0.0378 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 21.930 on 15 degrees of freedom
## Residual deviance: 15.979 on 14 degrees of freedom
## AIC: 19.979
##
## Number of Fisher Scoring iterations: 4