4.3 Two-way ANOVA
Met een GLM kan je gemakkelijk extra verklarende variabelen toevoegen aan je statistisch model.
Als voorbeeld nemen we een dataset uit R zelf: ToothGrowth. Deze bevat de gegevens van een experiment waarbij de lengte van de groeicellen van tanden gemeten is bij ratten die verschillende doses vitamine C kregen in twee mogelijke manieren van toedienen (als vitamine-C-druppels of als sinaasappelsap). Je hebt dus twee verklarende factoren: dosis (dose) en soort supplement (supp).
Eerst de data laden:
data("ToothGrowth")Vervolgens eerst kijken hoe je data eruit ziet (wat voor soort variabelen):
str(ToothGrowth)## 'data.frame': 60 obs. of 3 variables:
## $ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
## $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
## $ dose: num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...Supp is een factor (dus categoriedata), maar dosis wordt gezien als interval/ratio. In dit geval willen we dosis als categoriedata nemen. Dat kan met de volgende functie:
ToothGrowth$dose <- factor(ToothGrowth$dose)Volgende stap is een figuur maken:
library(tidyverse)## Warning: package 'ggplot2' was built under R version 4.1.3## Warning: package 'tibble' was built under R version 4.1.3## Warning: package 'tidyr' was built under R version 4.1.3## Warning: package 'readr' was built under R version 4.1.3## Warning: package 'dplyr' was built under R version 4.1.3ToothGrowth %>%
ggplot(aes(dose, len, color = supp)) +
geom_point(position = position_dodge(0.9)) +
theme_classic()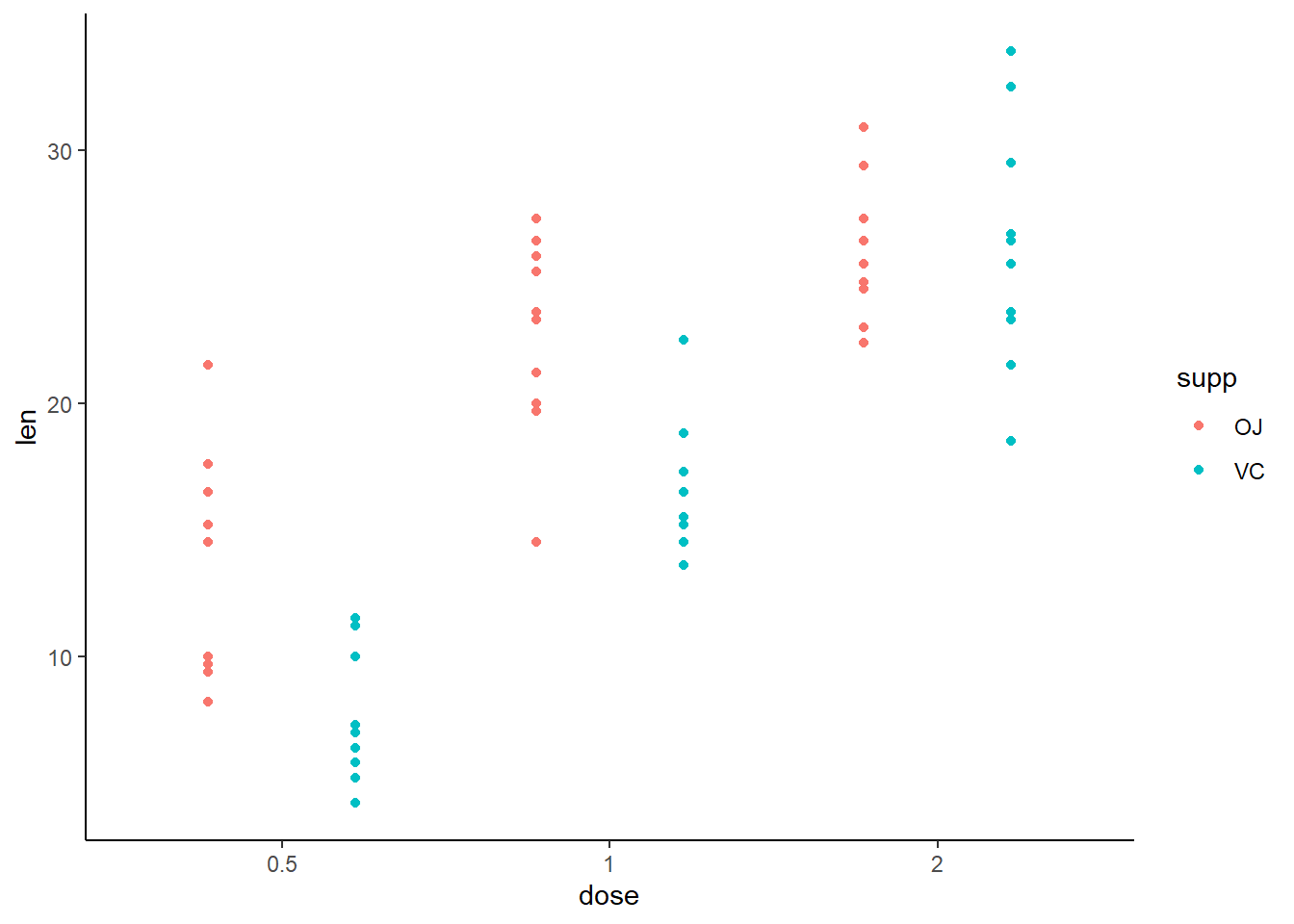
Zo op het eerste gezicht lijken beide variabelen (dose en supp) een effect te hebben op len. Dat gaan we testen met een two-way ANOVA, eerst zonder interacties:
fit <- lm(len ~ dose + supp, data = ToothGrowth)
anova(fit)## Analysis of Variance Table
##
## Response: len
## Df Sum Sq Mean Sq F value Pr(>F)
## dose 2 2426.43 1213.22 82.811 < 2.2e-16 ***
## supp 1 205.35 205.35 14.017 0.0004293 ***
## Residuals 56 820.43 14.65
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Beide verklarende variabelen hebben een significant effect op len.
We kunnen ook interacties tussen dose en supp onderzoeken. In plaats van + gebruik je *:
fit <- lm(len ~ dose * supp, data = ToothGrowth)
anova(fit)## Analysis of Variance Table
##
## Response: len
## Df Sum Sq Mean Sq F value Pr(>F)
## dose 2 2426.43 1213.22 92.000 < 2.2e-16 ***
## supp 1 205.35 205.35 15.572 0.0002312 ***
## dose:supp 2 108.32 54.16 4.107 0.0218603 *
## Residuals 54 712.11 13.19
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Een gemakkelijke functie om, nadat je een two-way ANOVA hebt uitgevoerd met interactie, ook de resultaten zonder interactie te bekijken:
drop1(fit, test = "F")## Single term deletions
##
## Model:
## len ~ dose * supp
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 712.11 160.43
## dose:supp 2 108.32 820.43 164.93 4.107 0.02186 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 14.3.1 Posthoc
Met een posthoc kan je, ook bij two-way ANOVA’s, testen welke groepen van elkaar verschillen. Omdat je nu meerdere verklarende variabelen hebt, moet je in de functie aangeven welke variabele je wilt testen:
emmeans(fit, specs = pairwise ~ dose)## NOTE: Results may be misleading due to involvement in interactions## $emmeans
## dose emmean SE df lower.CL upper.CL
## 0.5 10.6 0.812 54 8.98 12.2
## 1 19.7 0.812 54 18.11 21.4
## 2 26.1 0.812 54 24.47 27.7
##
## Results are averaged over the levels of: supp
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## dose0.5 - dose1 -9.13 1.15 54 -7.951 <.0001
## dose0.5 - dose2 -15.49 1.15 54 -13.493 <.0001
## dose1 - dose2 -6.37 1.15 54 -5.543 <.0001
##
## Results are averaged over the levels of: supp
## P value adjustment: tukey method for comparing a family of 3 estimatesIdem Bonferroni:
emmeans(fit, specs = pairwise ~ dose, adjust = "bonf")## NOTE: Results may be misleading due to involvement in interactions## $emmeans
## dose emmean SE df lower.CL upper.CL
## 0.5 10.6 0.812 54 8.98 12.2
## 1 19.7 0.812 54 18.11 21.4
## 2 26.1 0.812 54 24.47 27.7
##
## Results are averaged over the levels of: supp
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## dose0.5 - dose1 -9.13 1.15 54 -7.951 <.0001
## dose0.5 - dose2 -15.49 1.15 54 -13.493 <.0001
## dose1 - dose2 -6.37 1.15 54 -5.543 <.0001
##
## Results are averaged over the levels of: supp
## P value adjustment: bonferroni method for 3 tests